Il bilanciamento delle reazioni chimiche
Ora che sappiamo dare il nome e ricavare le formule dei principali composti chimici possiamo provare a scrivere e bilanciare le reazioni chimiche.
Per le reazioni chimiche vige il principio della conservazione della massa, secondo il quale “nulla si crea nulla si distrugge, ma tutto si trasforma”.
Ne consegue che il numero degli elementi che costituiscono i reagenti chimici deve essere del tutto uguale al numero degli stessi elementi che costituiscono i prodotti della reazione.
Facciamo un esempio, nel capitolo precedente abbiamo visto come dalla reazione di un ossido con acqua si ottenga un idrossido.
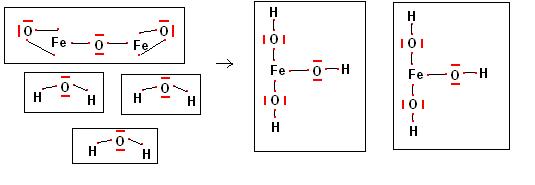
Dalla reazione tra ossido ferrico e acqua potremo quindi ottenere l’idrossido ferrico.
Scriviamo le formule dei composti chimici che prendono parte alla reazione.
Fe2O3 + H2O -> Fe(OH)3
Se consideriamo la reazione così come è scritta notiamo che a sinistra della freccia troviamo:
2 atomi di ferro, 2 atomi di idrogeno e 4 atomi di ossigeno (3 dell’ossido + 1 dell’acqua)
a destra della reazione troviamo invece:
1 atomo di ferro, 3 atomi di idrogeno e 3 atomi di ossigeno.
La reazione così come è scritta non risulta quindi bilanciata.
Per bilanciare la reazione dobbiamo per prima cosa tenere presente che non è possibile modificare la formula dei composti presenti.
Ad esempio non posso scrivere FeO al posto di Fe2O3 in quanto al posto del ossido ferrico mi troverei ad avere dell’ossido ferroso (una sostanza diversa).
Quello che è possibile fare è prendere più molecole di reagenti o di prodotti.
Ad esempio posso pensare che per questa reazione siano implicate due molecole di ossido ferrico e quindi mettere un 2 davanti al simbolo chimico di questo composto.
Si chiamano INDICI di reazioni i numeri che vengono messi davanti ai reagenti e prodotti per bilanciare una reazione chimica.
Ci sono diversi metodi per bilanciare le reazioni chimiche, ecco quello che consiglio per le reazioni più semplici (tutte quelle che prenderemo in considerazione in questo anno scolastico).
Torniamo alla nostra reazione campione
Fe2O3 + H2O -> Fe(OH)3
1.elenchiamo tutti gli elementi che partecipano alla reazione e che sono presenti sono in una molecola di reagente ed in una di prodotto:
Fe: reagente 2 prodotto 1
H : reagente 2 prodotto 3
ossigeno non preso in considerazione perchè presente in due molecole di reagenti.
2.Tra gli elementi selezionati consideriamo quello presente in numero pari da una parte ed in numero dispari dall’altra
3.Se come in questo caso ci sono due elementi che rispondono al requisito precedente si considera quello che è presente in quantità maggiore (in questo caso l’idrogeno).
4. selezioniamo le molecole che contengono l’elemento scelto ed invertiamo i coefficienti mettendo il numero di atomi presenti nel reagente davanti al prodotto e viceversa.
Fe2O3 + 3H2O -> 2Fe(OH)3
se contiamo ora il numero di idrogeni a destra e sinistra della reazione lo troveremmo uguale (6 atomi).
A questo punto non possiamo più toccare i coefficienti delle molecole che abbiamo sistemato altrimenti sbilanceremmo l’idrogeno.
5. dobbiamo ora mettere il coefficiente davanti alla molecola di Fe2O3.
Contiamo quanti atomi di ferro abbiamo ora a destra dove troviamo due molecole di Fe(OH)3.
Il numero di atomi di ferro nei prodotti è quindi 2 .
Dovremo quindi avere una sola molecola di Fe2O3.
Quando il coefficiente è 1 lo si omette per cui la reazione bilanciata diventa:
Fe2O3 + 3H2O -> 2Fe(OH)3
6. abbiamo messo i coefficienti davanti a tutte le molecole che partecipano alla reazione, per verificare che sia effettivamente bilanciata proviamo a contare gli ossigeni.
A sinistra 3 (dal Fe2O3) + 3 (dalle 3 molecole di H2O )= 6
A destra 6 (dalle due molecole di Fe(OH)3)
Quello che abbiamo a destra è uguale a quello che abbiamo a sinistra la reazione è quindi bilanciata.
Ecco come si legge la reazione:
Fe2O3 + 3H2O -> 2Fe(OH)3
Una molecola di ossido ferrico (formata da due atomi di ferro e tre di ossigeno) reagisce con 3 molecole di acqua (formata da due atomi di idrogeno e uno di ossigeno) per dare 2 molecole di idrossido ferrico (formato da un atomo di ferro, tre atomi di idrogeno e tre atomi di ossigeno).
Facciamo ora degli altri esempi:
Partiamo da un metallo qualsiasi (ad esempio il calcio) ed un non metallo qualsiasi (ad esempio il Fosforo).
Noi sappiamo che metallo + acqua da ossido; quindi Ca + Ossigeno = Ossido di calcio.
Formula del Ossido di calcio CaO
L’ossigeno è un gas biatomico = O2
Reazione non bilanciata
Ca + O2 -> CaO
il calcio a sinistra è uguale al calcio a destra.
Abbiamo due ossigeni a sinistra ed un ossigeno a destra.
Partiamo dall’ossigeno, metteremo un 2 davanti a CaO ed un 1 (si omette) davanti a O2.
Ca + O2 -> 2CaO
Rimane da mettere a posto il calcio, abbiamo ora due atomi di calcio a destra, quindi dovremo mettere un 2 davanti al Ca
2Ca + O2 -> 2CaO reazione bilanciata
Dalla reazione tra ossido di calcio e acqua otteniamo l’idrossido di calcio, formula Ca(OH)2
CaO + H2O -> Ca(OH)2
se contiamo gli atomi a destra li troviamo uguali a quelli di sinistra, la reazione è perciò già bilanciata
Passiamo ora al non metallo, il fosforo.
Il fosforo e del quinto gruppo, quindi può formare reagendo con l’ossigeno due anidridi: l’anidride fosforica o l’anidride fosforosa.
Immaginiamo che si formi l’anidride fosforica, formula chimica P2O5.
P + O2 -> P2O5 non bilanciata
Se contiamo gli atomi ci accorgiamo che conviene partire dall’ossigeno (2 atomi a sinistra, 5 atomi a destra).
Invertiamo i coefficienti ed avremo:
P + 5 O2 -> 2 P2O5
Ora ci troviamo ad avere 4 atomi di fosforo a destra, perciò il bilanciamento della reazione sarà:
4P + 5 O2 -> 2 P2O5 reazione bilanciata
L’anidride fosforica può reagire con l’acqua per dare l’acido metafosforico o l’acido ortofosforico, immaginiamo che si formi il secondo, formula chimica H3PO4.
P2O5 + H2O -> H3PO4 reazione non bilanciata.
se valutiamo gli elementi presenti escluderemo di partire dall’ossigeno (presente in due reagenti) e tra il fosforo e l’idrogeno considereremo meglio partire dall’idrogeno (2 atomi a sinistra e tre a destra).
Avremo quindi
P2O5 + 3H2O -> 2H3PO4
rimane da mettere a posto l’anidride fosforica, se contiamo gli atomi di fosforo a destra vediamo che sono 2 lo stesso numero degli atomi contenuti in una molecola di P2O5.
La reazione dovrebbe essere quindi già bilanciata, verifichiamo con gli ossigeni.
8 (5+3) atomi a sinistra , 8 (4×2) atomi a destra, tutto ok.
P2O5 + 3H2O -> 2H3PO4 reazione bilanciata
Nel capitolo precedente abbiamo detto che facendo reagire un composto derivante da un metallo, con uno derivante da un non metallo si ottiene sempre un sale.
Se facciamo reagire quindi l’ossido di calcio o l’idrossido di calcio con l’anidride fosforica o l’acido ortofosforico otterremo un sale che sarà: l’ortofosfato di calcio.
Per trovare la formula dell’ortofosfato di calcio dissociamo l’acido ortofosforico
H3PO4 -> 3H+ + PO4— il calcio è del secondo gruppo quindi Ca++
Avremo quindi Ca3(PO4)2
Vediamo ora le varie reazioni che posso utilizzare per ottenere questo sale (le riporto già bilanciate)
· ossido + anidride
3CaO + P2O5 -> Ca3(PO4)2
· ossido + acido
3CaO + 2H3PO4 -> Ca3(PO4)2 + 3H2O (notate la presenza dell’acqua)
· idrossido + anidride
3Ca(OH)2 + P2O5 -> Ca3(PO4)2 + 3H2O (notate la presenza dell’acqua)
· idrossido + acido
3Ca(OH)2 + 2H3PO4 -> Ca3(PO4)2 + 6H2O (notate la presenza dell’acqua)
Possiamo osservare che se uno dei reagenti contiene dell’idrogeno come prodotto si ottiene oltre che al sale dell’acqua.
E’ possibile ottenere un sale anche per reazione tra due sali, in questo caso si parla di reazioni di doppio scambio.
Immaginiamo di prendere due sali qualsiasi: ad esempio il cloruro di calcio ed il nitrato di argento.
· Il cloruro di calcio deriva dall’acido cloridrico (HCl)
Dissociamo l’acido HCl -> H+ + Cl– (ione cloruro)
Il calcio è del secondo gruppo avremo quindi lo ione Ca++
Il cloruro di sodio avrà quindi formula CaCl2
· Il nitrato di argento deriva dall’acido nitrico (HNO3)
Dissociamo l’acido HNO3-> H+ + NO3– (ione nitrato)
L’argento ha valenza uno, quindi sarà Ag+
Il nitrato di argento avrà quindi formula AgNO3
Cosa si potrà formare dalla reazione tra CaCl2 + AgNO3 ?
In pratica facendo avvenire questa reazione in acqua troveremo in soluzione i seguenti ioni
Ca++ ,Cl– ,Ag+ ,NO3–
Se combiniamo gli ioni positivi provenienti da un sale con gli ioni negativi provenienti dall’altro avremo:
AgCl (cloruro di argento) e Ca(NO3)2 (nitrato di calcio)
Si parla proprio di reazioni di doppio scambio in quanto i sali si scambiano gli ioni
La reazione sarà quindi:
CaCl2 + AgNO3 -> AgCl + Ca(NO3)2 non bilanciata
Bilanciandola con il solito metodo troveremo:
CaCl2 + 2AgNO3 -> 2AgCl + Ca(NO3)2
Come abbiamo visto le regole e le procedure per il bilanciamento delle reazioni di formazione degli ossidi, anidridi, idrossidi, acidi e sali sono abbastanza semplici.
Una volta capito il meccanismo base occorre però esercitarsi.
Sul libro di testo è possibile trovare molti esercizi di bilanciamento delle reazioni.
Masse atomiche, masse molecolari e numero di Avogadro
Prima di parlare effettivamente delle masse atomiche e molecolari facciamo dei piccoli esempi che sembrano non dover centrare nulla con la chimica.
Supponiamo di aver bisogno di un gran numero (diciamo un milione) di piccoli spilli, è possibile trovare un modo rapido per determinare questo numero senza dover contali uno a uno?.
Il metodo più logico è quello di dotarsi di una bilancia, se uno spillo è troppo piccolo per essere pesato, possiamo contare un certo numero di spilli tali da raggiungere un quantitativo rilevabile dal nostro strumento.
Immaginiamo che 100 spilli pesino 1,2 g.
A questo punto siamo in grado di determinare facilmente un peso in grammi di spilli tale da contenere un milione di questi oggetti:
100 spilli : 1,2 g = 1000000 spilli : x g x= 12000 g
Con questa proporzione possiamo quindi.
1. da un peso risalire al numero di spilli
2. prevedere il peso di un certo numero di spilli
Immaginiamo ora di avere due tipologie di spilli, una è quella che abbiamo visto nell’esempio precedente, l’altra è rappresentata da degli spilli che pesano due volte tanto.
Per avere un milione di spilli più grandi dovremo pesare il doppio del quantitativo di spilli che abbiamo calcolato in precedenza ossia 24000g
In altre parole avendo pesato un quantitativo doppio di un oggetto che pesa il doppio otteniamo sempre lo stesso numero di oggetti.
Torniamo ora alla chimica.
La tipologia di bilancia più sensibile che abbiamo misura un quantitativo di 0,00001g.
Un atomo pesa un quantitativo in grammi di gran lunga inferiore a quello misurabile con una bilancia.
Ci troviamo quindi nelle condizioni di determinare il peso di un quantitativo di atomi piuttosto grande (vedi esempio degli spilli) in modo da ricavare una relazione tra numero di atomi e loro peso.
I chimici attraverso delle esperienze sono riusciti a stabilire la relazione tra i pesi dei diversi atomi.
Hanno quindi definito un atomo campione al quale hanno attribuito un valore di riferimento.
Questo atomo campione è l’isotopo 12 del carbonio ha cui hanno assegnato un valore di 12.
Ricordiamo che gli isotopi sono atomi che hanno lo stesso numero di protoni, ma diverso numero
di neutroni.
Un atomo che pesa il doppio del carbonio isotopo 12 avrà quindi un valore di 24.
Poichè ogni atomo si trova ad avere una peso relativa all’atomo campione quello che troviamo è una scala dei pesi relativi degli atomi.
Si parla quindi di peso atomico relativo o più correttamente di masse atomiche relative.
Nella tavola periodica sono riportate le masse atomiche di tutti gli atomi.
Ad esempio la massa atomica dell’idrogeno è 1,0079, quella del magnesio 24,305 etc.
I pesi atomici hanno in genere delle cifre decimali in quanto quasi tutti gli elementi hanno degli isotopi. Poichè gli isotopi hanno peso diverso ma lo stesso numero atomico ci troviamo ad avere uno stesso atomo con pesi differenti.
Viene quindi eseguita una media “pesata” che tiene conto delle percentuali con cui i vari isotopi sono presenti in natura e che origina i decimali indicati nelle masse atomiche.
Le masse atomiche relative non dovrebbero avere delle unità di misura (indicano solo quanto un atomo pesa rispetto ad un altro), tuttavia ad esse viene attribuita una unità che viene indicata con la lettera:
“u” = unità di massa atomica oppure “d” = dalton
Se al posto di un atomo ci troviamo a trattare con una molecola possiamo determinare abbastanza facilmente la sua massa molecolare sommando le masse degli atomi che la compongono.
Facciamo un esempio.
L’acqua ha formula H2O
massa atomica H = 1 x 2 atomi = 2u +
massa atomica O = 16x 1 atomo = 16u =
massa molecolare dell’acqua = 18u
I chimici sono riusciti a determinare il numero di atomi presenti in una quantità di 12 g di carbonio isotopo 12.
Si tratta di un numero molto grande pari a 6,02.10^23 atomi.
Ora che sappiamo che un quantitativo in grammi pari alla massa atomica del carbonio isotopo 12 contiene questo numero di atomi possiamo calcolare quanti atomi sono contenuti in un quantitativo in grammi pari alla massa atomica di un qualsiasi elemento.
Prendiamo ad esempio l’idrogeno, un atomo di questo elemento pesa 1/12 del carbonio.
Quanti atomi di idrogeno avremo se pesiamo 1/12 di 12 grammi (ossia 1g)?
Se abbiamo capito l’esempio degli spilli dovremo giungere alla conclusione che pesando un dodicesimo di un oggetto che pesa un dodicesimo il numero di oggetti rimane lo stesso.
Possiamo giungere alla conclusione che:
Ogni volta che si pesa una quantità in grammi pari alla massa atomica (o alla massa molecolare) e come se contassimo un numero di atomi (o di molecole) pari a 6,02.10^23 .
Questo numero “fisso” prende il nome di numero di Avogadro.
Siamo ora in grado si stabilire il peso di un atomo in grammi.
Prendiamo ad esempio l’idrogeno.
1 g di idrogeno contiene 6,02.10^23 atomi, quanto pesa un atomo?
Basta fare 1g : 6,02.10^23 atomi = 1,66. 10^-24g
Come possiamo vedere si tratta di un peso estremamente piccolo.
La mole e i calcoli stechiometrici
Torniamo a prendere una reazione chimica bilanciata:
3Ca(OH)2 + 2H3PO4 -> Ca3(PO4)2 + 6H2O
Abbiamo già visto che questa reazione può essere letta come:
3 molecole di idrossido di calcio reagiscono con 2 molecole di acido ortofosforico per dare una molecola di ortofosfato di calcio e 6 molecole di acqua.
Noi però non siamo obbligati a far reagire solo 3 molecole di idrossido di calcio.
Se ne reagissero 6 cosa succederebbe?
Ovviamente poichè 6 è il doppio di tre tutti i coefficienti verrebbero raddoppiati per cui diremmo che:
6 molecole di idrossido di calcio reagiscono con 4 molecole di acido ortofosforico per dare 3 molecole di ortofosfato di calcio e 12 molecole di acqua.
Possiamo quindi giungere alla conclusione che i coefficienti di reazione indicano i rapporti di una reazione chimica.
In pratica è come in una ricetta di cucina in cui gli ingredienti sono indicati per un certo numero di persone, ma è sempre possibile aumentare le dosi lasciando costanti i rapporti tra i pesi degli ingredienti.
Se abbiamo capito questo concetto non dovremmo avere difficoltà ad immaginare che possiamo mantenere i rapporti di reazione anche raggiungendo quantità di molecole pari al numero di Avogadro e concludere che:
3 x n°Avogadro molecole di idrossido di calcio reagiscono con
2 x n°Avogadro molecole di acido ortofosforico per dare
1 x n°Avogadro molecole di ortofosfato di calcio e
6 x n°Avogadro molecole di acqua.
Definiamo mole un numero di atomi o molecole pari al numero di Avogadro.
Una mole non è quindi che un multiplo non decimale del numero di atomi o di molecole.
Tornando alla nostra reazione di esempio potremo quindi concludere che
3 moli di idrossido di calcio reagiscono con 2 moli di acido ortofosforico per dare una mole di ortofosfato di calcio e 6 moli di acqua.
Il vantaggio di usare le moli è quello di avere la possibilità di avere a che fare con quantità pesabili con la bilancia e di potere risalire in ogni istante al numero di atomi o molecole in gioco.
Moltiplicando il numero di moli per il numero di Avogadro si ottiene infatti il numero di atomi o di molecole.
Ma quanto pesa una mole?
La risposta dovrebbe essere evidente, ma proviamo a ricostruire il ragionamento fin qui fatto:
· un quantitativo in grammi pari alla massa atomica o molecolare contiene un numero di Avogadro di particelle
· un numero di Avogadro di particelle corrisponde ad una mole
Possiamo quindi definire una mole come una quantità in grammi pari alla massa atomica o molecolare.
In altre parole per ricavare il numero di moli è sufficiente eseguire la seguente operazione:
Moli = grammi sostanza / massa atomica (o molecolare)
Utilizziamo nuovamente la nostra reazione di esempio:
3Ca(OH)2 + 2H3PO4 -> Ca3(PO4)2 + 6H2O
determiniamo le masse molecolari:
Ca = 40 u O = 16 u H = 1 u P = 31 u
massa molecolare Ca(OH)2 = 74 u
massa molecolare H3PO4 = 98 u
massa molecolare Ca3(PO4)2 = 310 u
massa molecolare H2O = 18 u
immaginiamo ora di pesare 45g di idrossido di calcio possiamo prevedere con quanti grammi di acido ortofosforico reagiscono e quanti grammi di prodotti si possono ottenere?.
La risposta ovviamente è affermative ed ecco come si può risolvere il problema.
· Calcoliamo il numero di moli di idrossido di calcio applicando la relazione
moli = grammi sostanza / massa molecolare
i grammi sono 45g la massa molecolare 74 u quindi:
moli Ca(OH)2 = 45 / 74 = 0,61
· Guardiamo la reazione bilanciata ed osserviamo i rapporti stechiometrici notiamo che:
3 moli di idrossido reagiscono con due moli di acido ortofosforico
3 moli di idrossido formano 1 mole di ortofosfato di calcio
3 moli di idrossido formano 6 moli di acqua
Noi però non abbiamo 3 moli di idrossido bensì solo 0,61 ecco quindi le proporzioni che dobbiamo fare:
Moli di H3PO4 = 3moli : 2moli = 0,61moli : x x = 0,61 * 2 /3 = 0,41 moli
Moli di Ca3(PO4)2 = 3moli : 1moli = 0,61moli : x x = 0,61 * 1 /3 = 0,20 moli
Moli di H2O = 3moli : 6moli = 0,61moli : x x = 0,61 * 6 /3 = 1,22 moli
· Se moli = grammi/ peso molecolare possiamo dire che:
grammi sostanza = moli x peso molecolare
Avremo quindi:
grammi di H3PO4 = 0,41 moli x 98 u = 40 g
grammi di Ca3(PO4)2 = 0,20 moli x 310 u = 63 g
grammi di H2O = 1,22 moli x 18 u = 22 g
Se adesso sommiamo il peso dei reagenti Ca(OH)2 + H3PO4 troveremo = 45g + 40 g = 85 g
Pesando i reagenti Ca3(PO4)2 + H2O troveremo = 63 g + 22 g = 85 g.
Come si può osservare il peso dei reagenti è uguale al peso dei prodotti confermando il principio di conservazione della massa applicabile alle trasformazioni chimiche.
Il problema che abbiamo visto è un esempio di problema stechiometrico.
In pratica attraverso le moli e il bilanciamento delle reazioni possiamo prevedere le quantità di reagenti che occorrono per una reazione ed i quantitativi di prodotti ottenibili.
Il reagente limitante
Immaginiamo di gestire il magazzino di una fabbrica di motorini.
Per produrre un motorino occorrono diversi pezzi che spesso non sono presenti in rapporti 1:1.
Ad esempio possiamo pensare che servano per ogni motorino 2 ruote , una catena e 120 bulloni di un certo diametro.
La domanda che ora ci poniamo è la seguente:
Se in magazzino abbiamo 120 catene 60 ruote e 480 bulloni quanti motorini siamo in grado di produrre?
Con 120 catene possiamo produrre 120 motorini (rapporto 1:1)
Con 60 ruote possiamo produrre 30 motorini (rapporto 2:1)
con 480 bulloni possiamo produrre 4 motorini (rapporto 120:1).
Il numero massimo di motorini che possiamo produrre è quindi 4.
Notiamo che questo numero è dovuto al numero di bulloni che rappresenteranno il pezzo che limita la produzione.
Notiamo, inoltre, che in termini assoluti il numero di bulloni è il più alto (480), ma questo non impedisce che sia pur sempre il pezzo limitante.
Quello che dobbiamo considerare non è, infatti, solo il numero di pezzi che abbiamo, ma anche quanti pezzi servono per produrre una unità completa.
Ovviamente una volta prodotti i 4 motorini, nel magazzino rimarranno delle catene e delle ruote non utilizzate (in eccesso rispetto al pezzo limitante).
L’esempio che abbiamo fatto riferendoci ai motorini è facilmente applicabile anche alle reazioni chimiche.
Immaginiamo di avere una reazione bilanciata, ad esempio:
2Fe + 3S -> Fe2S3
Possiamo pensare che il prodotto della reazione (solfuro ferrico) sia il nostro “motorino”
ed il ferro e lo zolfo siano due pezzi che lo compongono.
Per fare il nostro prodotto occorrono 2 “pezzi” di ferro e 3 “pezzi di zolfo”
Supponiamo di avere nel nostro magazzino 25g di ferro e 30 grammi di zolfo e ci chiediamo quanti grammi di Fe2S3 possiamo produrre, ecco come operiamo:
· per prima cosa stabiliamo le masse atomiche e molecolari:
Fe = 56 u
S = 32 u
Fe2S3= 208 u
· Stabiliamo le moli di ferro e di zolfo in base ai grammi che abbiamo
moli di ferro = 25 g / 56u = 0,45
moli di zolfo = 30 g / 32u = 0,93
notiamo che le moli di zolfo sono di più di quelle di ferro, ma ciò non è sufficiente a stabilire che esso non è il reagente limitante.
· Stabiliamo quante moli di prodotto si possono ottenere dai valori di moli dei reagenti
moli di solfuro ottenibili da ferro = 0,45 : 2 = 0,225 (rapporto 2:1)
moli di solfuro ottenibili da zolfo = 0,93 :3 = 0,31 (rapporto 3:1)
Abbiamo stabilito che con i quantitativi che abbiamo il ferro origina meno solfuro di quanto se ne può originare dallo zolfo.
Il ferro è quindi il reattivo limitante.
Le moli di solfuro ferrico che possiamo produrre saranno quindi solo 0,225 che corrispondono ad un peso di questa sostanza pari a:
grammi = moli x peso molecolare = 0,225 x 208 = 46,8 grammi.
al termine della reazione rimarrà una certa quantità di zolfo che non ha reagito.